
「バラツキを小さくする」ことと「被験者数を増やす」ことの関係性
前回、丁寧に試験を行ってバラツキを小さくすると、同等性が成立しやすいというお話をしました。同じように同等性試験は、被験者数を増やすと同等性が成立しやすい性質があります。
では、バラツキを小さくすることと、被験者数を増やすことは、どのような関係にあるか知っていますか。
ずばりお答えしましょう。
バラツキを2分の1にすることは、被験者数を4倍にすることと同じ影響があります。
さらに言いますと、バラツキを3分の1にすることは、被験者数を9倍にすることに匹敵します。
被験者数を4倍にするためには、治験費用が約4倍になります。しかし、バラツキを半分にすることなら、丁寧にやることで達成できる場合が多いのです。
ただ、さすがにバラツキを3分の1にするのは大変です。したがって私は、いつも、丁寧に同等性試験を行ってバラツキを半分にして、試験の価値を4倍にすることを目指しています。
今回覚えていただきたいことはこれだけです。
この内容については、以下で詳しく述べますが、数学・統計・理屈の好きな人以外は、あとがきに進んでください。とにかく難しいからです。
試験製剤と標準製剤の同等性の判定基準
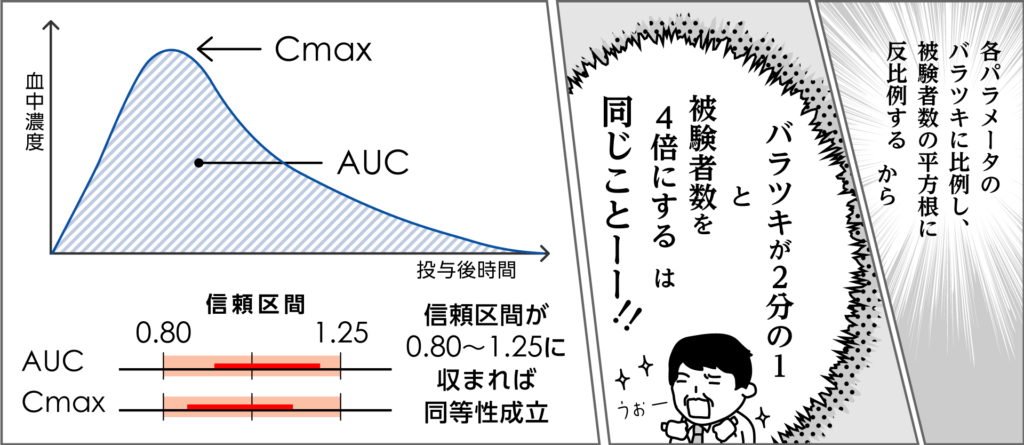
『試験製剤と標準製剤の生物学的同等性判定パラメータの対数値の平均値の差の90%信頼区間が、log(0.80)~log(1.25)の範囲にあるとき、試験製剤と標準製剤は同等と判定する』
上の文章は同等性のガイドラインの最も重要な部分です。
私は、同等性試験の仕事を25年もしております。当然、上記の同等性試験のガイドラインの文章は理解できています……と言いたいところですが、残念ながら完全には理解できていません。
ところが数ヵ月前に、大学の薬学部の学生さん向けに授業をする機会があり、この説明をすることになりました。
ここで、苦しいながらも授業で行った際の説明を用いて、先の「バラツキを2分の1にすることは、被験者数を4倍にすること同じ」の解説をしたいと思います。
同等性試験では、標準製剤と新規製剤を各被験者に投与して、それぞれのACUとCmaxのデータを集めて、信頼区間を算出します。
信頼区間は次のような式で表されます。
信頼区間 ≒ A ± B
(対数は無視して説明を続けます)
Aは、標準製剤のパラメータの平均値に対する新規製剤のパラメータの平均値の比です。平均値が一致する理想的な場合にはAは1になります。
Bは、各パラメータのバラツキに比例し、被験者数の平方根に反比例します。
この信頼区間が0.80~1.25の範囲に入っているときに、同等性が成立したと判定されます。
Bが各パラメータのバラツキに比例し、被験者数の平方根に反比例することから、バラツキが2分の1になることと、被験者数を4倍にすることは信頼区間の幅に対して同じ意味をもつことになります。
説明は以上です。
この部分を読んでくださった方、ありがとうございました。
もし、この辺の説明に詳しい方がいましたら、何かのときにいろいろ教えていただけたら幸いです。

あとがき
前回のこのコラムに大変な反響をいただきありがとうございました。
A社のモニターの女性が駆け寄ってこられて「読みましたよ」と、満面の笑みで話しかけられたときは、芸能人になったような気分でした。このまま小説家を目指そうかと思ったくらいです。B社の方からは「私たちはいつ登場するのですか」というメールをいただき、「3回目に登場していただきます」と咄嗟に答えてしまい、急遽、次回までにストーリーを考えることになりました。意外だったのは、最近よく治験に参加している30歳代の漫画家志望のC君が「僕にも読ませてください。内容がわからなくても調べますから」と熱心に言ってくれたことです。
このコラムは、製薬会社の方に見てもらって、あわよくばお仕事をいただこうという趣旨でしたが、少しだけ軌道修正して、なるべくいろんな立場の人にも読んでもらえるようにがんばりたいと思います。
(公開日:2023年10月24日)
筆者プロフィール:
古家英寿
医療法人平心会 大阪治験病院
日本臨床薬理学会(専門医・指導医・評議員)
日本内科学会認定総合内科専門医
大阪大学医学部 特任准教授
